ПОВЕРХНОСТНОЕ МОДЕЛИРОВАНИЕ В КОМПАС 3D. Маховичок
1,315 просмотров
22.11.2024
34 0

Школа САПР Анны Веселовой
Урок посвящен моделированию в Компас 3D детали с криволинейной поверхностью. Адаптация моделирования для Компас (изначальная модель проектировалась в Fusion 360)
ПРЕДЗАПИСЬ НА КУРС КОМПАС 3D - https:...
ПРЕДЗАПИСЬ НА КУРС КОМПАС 3D - https:...
 Возрастное ограничение 12+
Возрастное ограничение 12+
Комментарии (2)
Рекомендуемые видео

Цепь. Управление массивом при помощи логических операций
Школа САПР Анны Веселовой95 просмотров
Обзор как настроить и подключить терморегулятор STC 1000
Настройка теплого пола и терморегулятора4,484 просмотров
Создание виртуальной машины с Ubuntu в Proxmox
ProHomelab432 просмотров

Алюминиевые хардтейлы Corratec 2024. Обзор линейки
Триал-Спорт634 просмотров
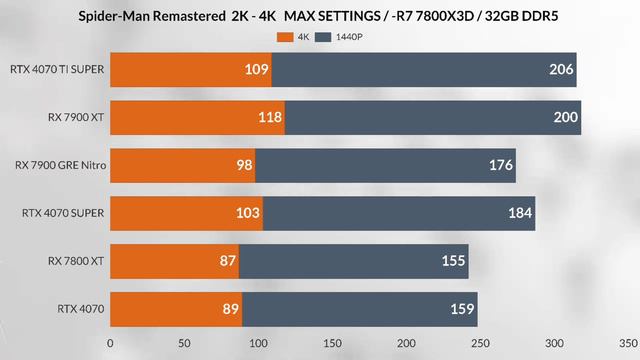
7900 gre vs 7800 xt vs rtx 4070 Vs RTX 4070 super vs RTX 4070 TI super VS 1440p + 2K gaming test
Игровые обзоры: подробности и детализация119 просмотров

Контурная пластика "ANTI-AGE"
TORI CLINIC226 просмотров

Новинки «СёрчИнформ» 2024
ИБ от «СёрчИнформ»110 просмотров

«Вопросы священнику» с иереем Сергием Тарасовым
Просветительский проект " Ходынский вестник"138 просмотров
ПОВЕРХНОСТНОЕ МОДЕЛИРОВАНИЕ В КОМПАС 3D. Маховичок - смотреть онлайн
Смотрите видео "ПОВЕРХНОСТНОЕ МОДЕЛИРОВАНИЕ В КОМПАС 3D. Маховичок" онлайн бесплатно в HD качестве. Школа САПР Анны Веселовой представляет вашему вниманию качественный контент, доступный для просмотра без регистрации.
О видео
Урок посвящен моделированию в Компас 3D детали с криволинейной поверхностью. Адаптация моделирования для Компас (изначальная модель проектировалась в Fusion 360) ПРЕДЗАПИСЬ НА КУРС КОМПАС 3D - https://cadprosto.ru/predzapis-kompas-1 Ознакомиться с программой обучения САПР Компас 3D (V17-V23) - ht...
Смотрите также
Если вам понравилось видео "ПОВЕРХНОСТНОЕ МОДЕЛИРОВАНИЕ В КОМПАС 3D. Маховичок", рекомендуем посмотреть другие работы от Школа САПР Анны Веселовой или похожие видео в категории Обучение.
Анатолий Рождествин
04.12.2024Массив эскиза основания не нужен, так как для разбиения вертикальной поверхности перпендикулярной основанию подойдёт любой отрезок построенный на этом основании и имеющий общую точку с разбиваемой поверхностью.
Анатолий Рождествин
28.11.2024Что-то мне подсказывает , что это единственный метод. Надо классно знать Компас. Пробовал построить по-другому - пока не получилось, постоянно наталкиваюсь на какие-нибудь ограничения. Буду пробовать, в том числе и в других системах.